The Lost Boarding Pass puzzle

The puzzle:

One hundred passengers are about to board a plane. The first passenger lost his boarding pass and decides to choose a seat randomly. Each subsequent passenger sits in their assigned seat if it is free or chooses a seat randomly from those remaining.

What is the probability that the last passenger will get to sit in his assigned seat?

Despite the fact that this puzzle lead me on a wild goose chase, I do have a soft spot for it. The reason is that after reading the solution given by Peter Winkler in his book:Mathematical Puzzles (A Connoisseur’s Collection)

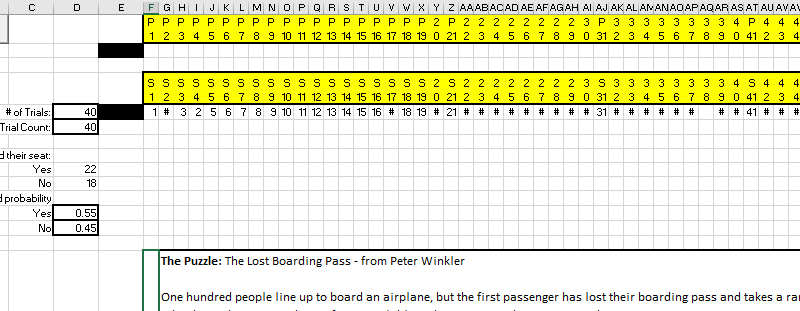
I was so convinced he was wrong I decided to test it using a simple computer model. Thus started my adventure with Excel VBA in earnest, which continues to this day. The principle was simple, follow the rules of the puzzle in an excel sheet and see how many times the last passenger had their own seat.

If you have Excel on your computer, feel free to give it a whirl: lost-boarding-pass-puzzle However, keep in mind that it uses VBA so security warnings are likely.

Unfortunately I only succeeded in proving Winkler right and myself wrong. The answer is: as Winkler states, 50%.

In hindsight it is hard to see how I could of thought otherwise. It seems the puzzle uses a bit of misdirection and leads the puzzler to focus on an area of zero relevance.

Considering how the seating pattern affects the outcome is offtrack.

The result is determined when someone looking for a new seat either sits in their own seat or the seat of the last passenger to board. Right from the first passenger, the probability of sitting in either of these two seats is equal and the puzzle only ends when one of the two seats is taken. All other passengers who select a different seat have no impact on the outcome. They simple kick the can further down the line.